Décryptage des symboles mathématiques : un guide pour les débutants
Vous vous êtes déjà retrouvé face à une équation mathématique remplie de symboles étranges et incompréhensibles ? Vous vous êtes peut-être demandé : « Que signifie ce symbole en maths ? » Pas de panique ! Ce guide est là pour vous aider à déchiffrer le langage des mathématiques et à comprendre la signification de ces symboles mystérieux.
Les symboles mathématiques : un langage universel
Les mathématiques sont un langage universel, et comme tout langage, elles ont leurs propres symboles. Ces symboles sont des raccourcis qui permettent de représenter des concepts mathématiques complexes de manière concise et efficace. Ils sont utilisés dans tous les domaines des mathématiques, de l’arithmétique à l’algèbre, en passant par la géométrie et le calcul.
Comprendre la signification de ces symboles est essentiel pour pouvoir lire, comprendre et utiliser les mathématiques.
Les symboles les plus courants en mathématiques
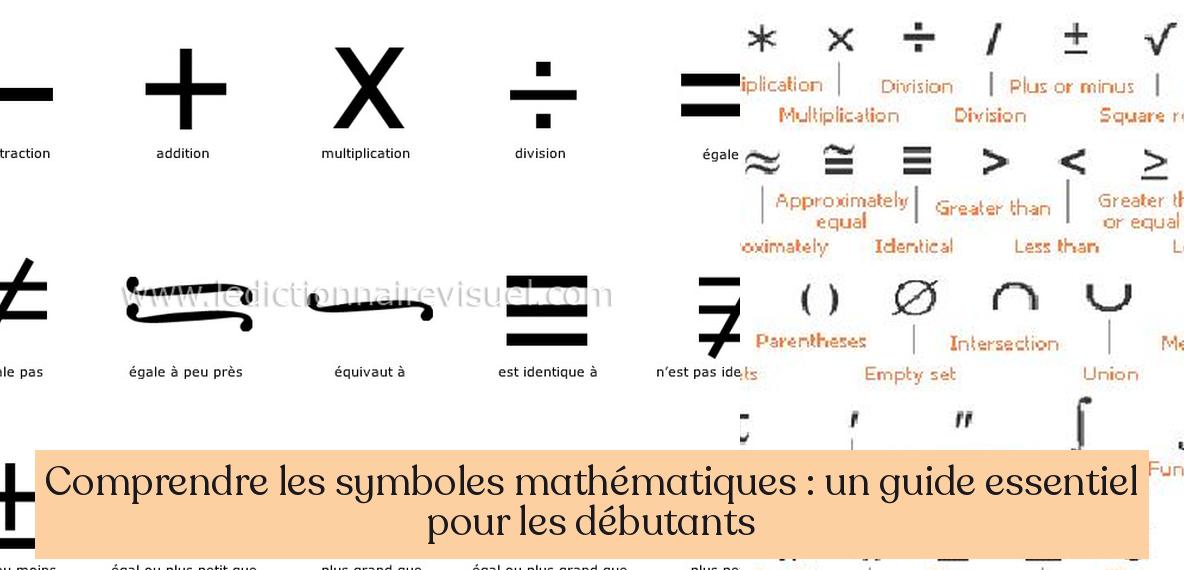
Voici une liste des symboles mathématiques les plus courants, avec leur signification et des exemples d’utilisation :
- = (Égalité) : Ce symbole signifie que deux expressions ont la même valeur.
- Exemple : 2 + 3 = 5
- > (Supérieur à) : Ce symbole signifie que le nombre à gauche est plus grand que le nombre à droite.
- Exemple : 5 > 3
- < (Inférieur à) : Ce symbole signifie que le nombre à gauche est plus petit que le nombre à droite.
- Exemple : 3 < 5
- ≥ (Supérieur ou égal à) : Ce symbole signifie que le nombre à gauche est plus grand ou égal au nombre à droite.
- Exemple : 5 ≥ 5
- ≤ (Inférieur ou égal à) : Ce symbole signifie que le nombre à gauche est plus petit ou égal au nombre à droite.
- Exemple : 3 ≤ 5
- ≠ (Différent de) : Ce symbole signifie que deux expressions n’ont pas la même valeur.
- Exemple : 2 + 3 ≠ 6
- + (Addition) : Ce symbole représente l’opération d’addition.
- Exemple : 2 + 3 = 5
- – (Soustraction) : Ce symbole représente l’opération de soustraction.
- Exemple : 5 – 3 = 2
- × (Multiplication) : Ce symbole représente l’opération de multiplication.
- Exemple : 2 × 3 = 6
- ÷ (Division) : Ce symbole représente l’opération de division.
- Exemple : 6 ÷ 2 = 3
- √ (Racine carrée) : Ce symbole représente la racine carrée d’un nombre.
- Exemple : √9 = 3
- % (Pourcentage) : Ce symbole représente une fraction de 100.
- Exemple : 50% = 50/100 = 0.5
- π (Pi) : Ce symbole représente le rapport de la circonférence d’un cercle à son diamètre.
- Exemple : π ≈ 3.14159
- e (Nombre d’Euler) : Ce symbole représente la base des logarithmes naturels.
- Exemple : e ≈ 2.71828
- ∞ (Infini) : Ce symbole représente un nombre infiniment grand.
- Exemple : 1/∞ = 0
- ∈ (Appartient à) : Ce symbole signifie qu’un élément appartient à un ensemble.
- Exemple : 2 ∈ {1, 2, 3}
- ∉ (N’appartient pas à) : Ce symbole signifie qu’un élément n’appartient pas à un ensemble.
- Exemple : 4 ∉ {1, 2, 3}
- ⊆ (Sous-ensemble) : Ce symbole signifie qu’un ensemble est un sous-ensemble d’un autre ensemble.
- Exemple : {1, 2} ⊆ {1, 2, 3}
- ⊂ (Sous-ensemble strict) : Ce symbole signifie qu’un ensemble est un sous-ensemble strict d’un autre ensemble.
- Exemple : {1, 2} ⊂ {1, 2, 3}
- ∑ (Somme) : Ce symbole représente la somme d’une série de nombres.
- Exemple : ∑(i=1 à 3) i = 1 + 2 + 3 = 6
- ∏ (Produit) : Ce symbole représente le produit d’une série de nombres.
- Exemple : ∏(i=1 à 3) i = 1 × 2 × 3 = 6
- ∫ (Intégrale) : Ce symbole représente l’intégrale d’une fonction.
- Exemple : ∫(x=0 à 1) x² dx = 1/3
- d/dx (Dérivée) : Ce symbole représente la dérivée d’une fonction par rapport à x.
- Exemple : d/dx (x²) = 2x
Apprendre à lire les symboles mathématiques
Comprendre la signification des symboles mathématiques est une étape cruciale pour déchiffrer les équations et les formules. Mais il est également important de savoir comment les lire.
- Lisez les symboles de gauche à droite.
- Utilisez les mots « est égal à », « est supérieur à », « est inférieur à » pour lire les symboles d’égalité et d’inégalité.
- Utilisez les mots « plus », « moins », « multiplié par », « divisé par » pour lire les symboles d’opération.
- Pratiquez régulièrement la lecture des symboles pour vous familiariser avec leur signification.
Les lettres grecques en mathématiques
Les lettres grecques sont souvent utilisées en mathématiques pour représenter des constantes, des variables et des fonctions. Voici quelques-unes des lettres grecques les plus courantes en mathématiques :
- α (alpha) : utilisé pour représenter un angle ou une constante.
- β (bêta) : utilisé pour représenter un angle ou une constante.
- γ (gamma) : utilisé pour représenter un angle, une constante ou une fonction.
- δ (delta) : utilisé pour représenter un incrément, un changement ou une fonction.
- ε (epsilon) : utilisé pour représenter un nombre infiniment petit ou une erreur.
- ζ (zêta) : utilisé pour représenter une variable ou une fonction.
- η (êta) : utilisé pour représenter une variable ou une fonction.
- θ (thêta) : utilisé pour représenter un angle ou une variable.
- λ (lambda) : utilisé pour représenter une longueur d’onde, une constante ou une fonction.
- μ (mu) : utilisé pour représenter une moyenne, une constante ou une fonction.
- ν (nu) : utilisé pour représenter une fréquence, une constante ou une fonction.
- ξ (xi) : utilisé pour représenter une variable ou une fonction.
- π (pi) : utilisé pour représenter le rapport de la circonférence d’un cercle à son diamètre.
- ρ (rho) : utilisé pour représenter une densité, une constante ou une fonction.
- σ (sigma) : utilisé pour représenter une déviation standard, une constante ou une fonction.
- τ (tau) : utilisé pour représenter un temps, une constante ou une fonction.
- ϕ (phi) : utilisé pour représenter un angle, une constante ou une fonction.
- χ (khi) : utilisé pour représenter une variable ou une fonction.
- ψ (psi) : utilisé pour représenter une fonction ou une variable.
- ω (oméga) : utilisé pour représenter une fréquence angulaire, une constante ou une fonction.
Des exemples concrets pour mieux comprendre
Pour illustrer l’utilisation des symboles mathématiques, voici quelques exemples concrets :
- « x + y = 5 » : Cette équation signifie que la somme de deux variables, x et y, est égale à 5.
- « f(x) = x² » : Cette fonction signifie que la valeur de f(x) est égale au carré de x.
- « ∫(x=0 à 1) x² dx = 1/3 » : Cette intégrale signifie que l’aire sous la courbe de la fonction f(x) = x² entre x = 0 et x = 1 est égale à 1/3.
Conclusion : la clé du succès en mathématiques
Comprendre la signification des symboles mathématiques est la clé du succès en mathématiques. En vous familiarisant avec ces symboles, vous pourrez déchiffrer les équations et les formules, et ainsi mieux comprendre les concepts mathématiques. N’hésitez pas à consulter des ressources en ligne ou des livres pour approfondir vos connaissances et à pratiquer régulièrement la lecture et l’utilisation des symboles mathématiques.
N’oubliez pas que les mathématiques ne sont pas un obstacle, mais un outil puissant pour comprendre le monde qui nous entoure.
Que sont les symboles mathématiques et pourquoi sont-ils importants ?
Les symboles mathématiques sont des raccourcis utilisés pour représenter des concepts mathématiques de manière concise. Ils sont essentiels pour lire, comprendre et utiliser les mathématiques.
Quels sont quelques-uns des symboles mathématiques les plus courants et leur signification ?
Quelques symboles mathématiques courants incluent = (égalité), > (supérieur à), < (inférieur à), ≥ (supérieur ou égal à), ≤ (inférieur ou égal à), ≠ (différent de), + (addition) et – (soustraction).
Comment peut-on interpréter le symbole = en mathématiques ?
Le symbole = signifie que deux expressions ont la même valeur. Par exemple, 2 + 3 = 5 indique que 2 plus 3 est égal à 5.
Quelle est la signification du symbole > en mathématiques et pouvez-vous donner un exemple ?
Le symbole > signifie « supérieur à », indiquant que le nombre à gauche est plus grand que celui à droite. Par exemple, 5 > 3 signifie que 5 est plus grand que 3.