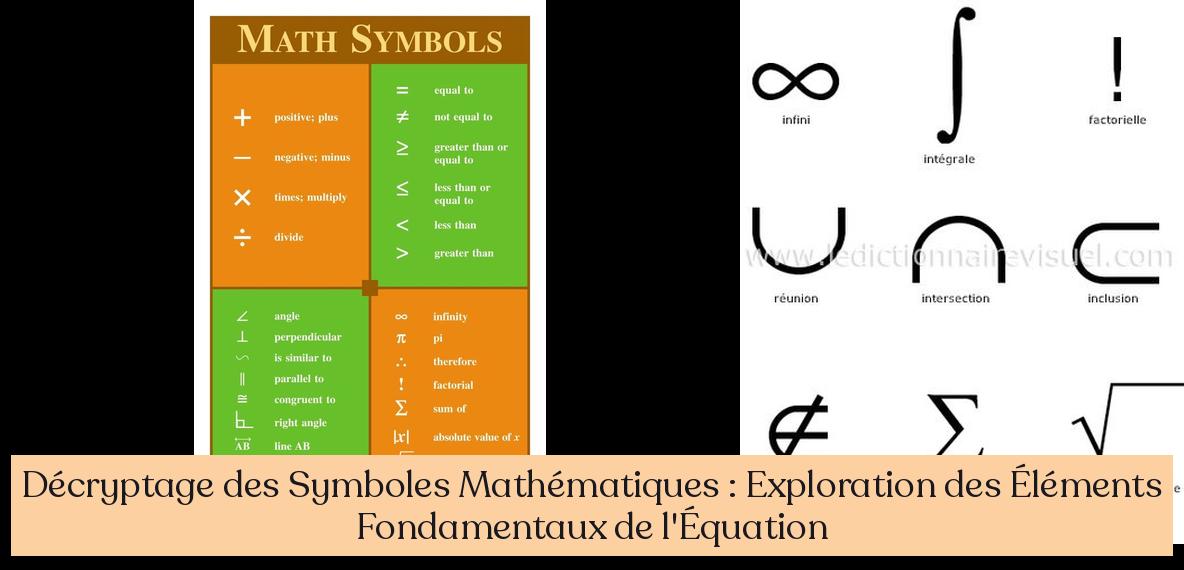
Décryptage des Symboles Mathématiques : Un Voyage au Cœur des Équations
Le monde des mathématiques est un univers fascinant rempli de symboles énigmatiques qui, à première vue, peuvent sembler intimidants. Mais derrière ces signes mystérieux se cachent des concepts profonds et des relations mathématiques complexes. Imaginez un langage universel, où chaque symbole porte un poids précis, une signification unique qui ouvre la porte à des vérités mathématiques universelles. C’est précisément ce que représente le langage des symboles mathématiques.
Dans ce voyage au cœur des équations, nous allons démystifier certains des symboles mathématiques les plus courants et explorer leur signification profonde. Préparez-vous à découvrir un langage fascinant qui révèle la beauté et la puissance des mathématiques.
Imaginez une équation complexe, une mosaïque de symboles qui se succèdent, une symphonie de signes qui se combinent pour révéler une vérité mathématique. Chaque symbole, comme une note de musique, joue un rôle crucial dans l’harmonie de l’équation.
Comprendre la signification de ces symboles est essentiel pour déchiffrer le langage des mathématiques. C’est comme déchiffrer un code secret, où chaque symbole dévoile une nouvelle facette de la réalité mathématique.
Alors, embarquez avec nous dans cette exploration passionnante du monde des symboles mathématiques. Préparez-vous à être surpris par la profondeur et la beauté des concepts mathématiques qui se cachent derrière ces signes énigmatiques.
Les Signes d’Inégalité : Un Jeu de Plus Grand et de Plus Petit
Imaginez deux nombres, l’un plus grand que l’autre. Comment exprimer cette relation de manière concise et universelle ? C’est là qu’intervient l’ingéniosité des signes d’inégalité : > et <. Ces deux symboles, simples mais puissants, sont les clés pour comprendre les relations d’ordre entre les nombres.
Le signe >, qui ressemble à une bouche ouverte vers la droite, signifie « plus grand que« . Il indique que le nombre situé à gauche du signe est supérieur au nombre situé à droite. Par exemple, 5 > 3 signifie que 5 est plus grand que 3.
À l’inverse, le signe <, qui ressemble à une bouche ouverte vers la gauche, signifie « plus petit que« . Il indique que le nombre situé à gauche du signe est inférieur au nombre situé à droite. Par exemple, 3 < 5 signifie que 3 est plus petit que 5.
Ces signes d’inégalité sont utilisés dans de nombreux domaines des mathématiques, de l’algèbre à l’analyse, pour exprimer des relations d’ordre entre les nombres, les variables et les expressions mathématiques.
Imaginez un jeu de comparaison, où vous devez déterminer quel nombre est le plus grand. Les signes d’inégalité sont vos alliés pour naviguer dans ce jeu et trouver la solution avec précision.
L’Alphabet Grec : Un Code Secret pour les Mathématiques
L’alphabet grec est un trésor de symboles qui ont transcendé les frontières de la langue et sont devenus des éléments fondamentaux du langage des mathématiques. Des lettres comme α (alpha), β (bêta), γ (gamma), δ (delta) et bien d’autres sont devenues des symboles incontournables dans de nombreux domaines des mathématiques.
Ces lettres grecques ne sont pas seulement des symboles décoratifs, mais des éléments essentiels pour représenter des concepts mathématiques importants. Elles sont utilisées pour désigner des variables, des constantes, des fonctions, des angles, des vecteurs et bien plus encore.
Imaginez un langage secret, où chaque lettre grecque représente un concept mathématique spécifique. C’est ainsi que l’alphabet grec est utilisé en mathématiques, un code secret qui permet aux mathématiciens de communiquer et de partager des idées d’une manière concise et universelle.
Prenons l’exemple du symbole π (pi), une lettre grecque qui représente la constante mathématique qui exprime le rapport entre la circonférence d’un cercle et son diamètre. Cette constante, d’une importance capitale en géométrie, est représentée par un symbole grec, un témoignage de l’influence de l’alphabet grec sur les mathématiques.
L’alphabet grec est une source de fascination pour les mathématiciens et les scientifiques. Il est un langage universel qui permet de communiquer des idées mathématiques complexes de manière claire et concise.
Le Symbole Vecteur : Un Voyage dans l’Espace
Imaginez un objet qui se déplace dans l’espace. Comment décrire sa direction et sa magnitude ? C’est là qu’intervient le concept de vecteur, un outil puissant en mathématiques pour représenter des grandeurs qui ont à la fois une direction et une intensité.
Le symbole vecteur, souvent représenté par une lettre surmontée d’une flèche, comme v, est utilisé pour représenter un vecteur. Cette flèche indique la direction du vecteur, tandis que la longueur de la flèche représente sa magnitude.
Les vecteurs sont utilisés dans de nombreux domaines des mathématiques, de la géométrie à la physique, pour représenter des grandeurs comme la vitesse, la force, le déplacement et bien plus encore.
Imaginez un avion qui vole dans le ciel. Sa vitesse est représentée par un vecteur, qui indique sa direction et sa magnitude. Le vecteur vitesse est un outil essentiel pour comprendre le mouvement de l’avion dans l’espace.
Le symbole vecteur est un outil puissant pour visualiser et comprendre les grandeurs qui ont à la fois une direction et une intensité. Il est un langage universel qui permet de décrire le mouvement et les interactions dans l’espace.
Le Symbole « ∈ » : L’Appartenance à un Ensemble
Imaginez un groupe d’objets, une collection d’éléments qui partagent une caractéristique commune. Comment exprimer l’appartenance d’un élément à ce groupe ? C’est là qu’intervient le symbole ∈, un symbole qui signifie « appartient à« .
Le symbole ∈ est utilisé pour indiquer qu’un élément fait partie d’un ensemble. Par exemple, si x ∈ {1, 2, 3}, cela signifie que x est un élément de l’ensemble {1, 2, 3}.
Imaginez un panier de fruits. Chaque fruit dans le panier appartient à l’ensemble des fruits. Le symbole ∈ permet de représenter cette relation d’appartenance de manière concise et universelle.
Le symbole ∈ est utilisé dans de nombreux domaines des mathématiques, de la théorie des ensembles à l’algèbre, pour exprimer l’appartenance d’un élément à un ensemble. Il est un outil essentiel pour comprendre les relations entre les éléments et les ensembles.
Le symbole ∈ est un langage universel qui permet de décrire les relations d’appartenance entre les éléments et les ensembles, un concept fondamental en mathématiques.
Le Symbole « e » : La Charge Élémentaire
Imaginez la plus petite unité de charge électrique, la brique élémentaire qui compose toute la charge électrique dans l’univers. Cette unité fondamentale est représentée par le symbole e, un symbole qui représente la charge élémentaire.
La charge élémentaire, d’une importance capitale en physique, est une constante physique qui représente la charge d’un électron ou d’un proton. Elle est définie comme 1,602 176 634 × 10−19 coulombs.
Imaginez un courant électrique qui traverse un fil. Ce courant est composé d’un flux d’électrons, chacun portant une charge élémentaire e. La charge élémentaire est la base de l’électricité et de l’électromagnétisme.
Le symbole e est un élément essentiel pour comprendre les phénomènes électriques et électromagnétiques. Il est un langage universel qui permet de décrire la charge électrique à l’échelle microscopique.
Le symbole e est un pont entre le monde microscopique des particules et le monde macroscopique des phénomènes électriques et électromagnétiques.
Conclusion : Un Langage Universel des Mathématiques
Le voyage au cœur des symboles mathématiques nous a permis de découvrir un langage fascinant, un code secret qui révèle des vérités mathématiques universelles. Chaque symbole, comme une pièce d’un puzzle, joue un rôle crucial dans la construction de l’édifice des mathématiques.
De l’alphabet grec aux signes d’inégalité, du symbole vecteur au symbole ∈, chaque symbole a sa propre histoire et sa propre signification. Ces symboles ne sont pas seulement des signes décoratifs, mais des outils puissants qui permettent aux mathématiciens de communiquer et de partager des idées d’une manière concise et universelle.
Comprendre le langage des symboles mathématiques est essentiel pour déchiffrer les mystères des équations et explorer les profondeurs du monde mathématique. C’est un voyage fascinant qui nous invite à découvrir la beauté et la puissance des mathématiques.
Que représentent les symboles mathématiques ?
Les symboles mathématiques représentent des concepts profonds et des relations mathématiques complexes.
Comment sont utilisés les signes d’inégalité en mathématiques ?
Les signes d’inégalité, > et <, sont utilisés pour exprimer les relations d’ordre entre les nombres.